233,евклид

Научная деятельность и открытия

Вся жизнь ученого прошла в александрийских стенах, поэтому и его научная деятельность с открытиями состоялась здесь. Образование он получил от платоновских учеников, поэтому от них же и перенял взгляды, которые и помогли ему сформировать свой класс математики и стать преподавателем.

Предшественниками Евклида были знаменитые математики Фалес с Пифагором и Аристотелем, которые сделали фундаментальные открытия в области тригонометрической науки. Но это были разрозненные части и не представляли собой одну большую логически выстроенную цепочку.

Как и современники, математик и его ученики любили систематичные и логичные знания. Именно поэтому всю свою научную деятельность Евклид бросил на систематизацию ранее полученных знаний и их дополнение. В каждой из своих книг «Начал» он дает основные понятия, использованные учеными ранее, а затем вводит основные аксиомы и постулаты геометрии, которые упростили работу его потомкам.

Так, с первой по четвертую книгу даются понятия и постулаты из трудов Пифагора и его последователей, в пятой книге — учение о пропорциях, с шестой по девятую книгу — знание о числах, а в последних — публикации о площадях с плоскостями и пространствами (основы стереометрии), иррациональности, учении о правильных телах.

Интересно, что публикация автора дала возможность писать последующие научные работы в области математики и получать новые знания о ней.

Свои открытия ученый сделал в той же области. Он ввел понятие точки, прямой, плоскости и движения, разработал постулаты для создания определенных геометрических фигур в любой области, понятие о свете, зеркалах, преломлении световых лучей, ввел элементарную теорию музыки, создал труд касательно использования геометрии при изучении астрономии и ошибках, которые возникают при формировании геометрических доказательств.

Кроме того, математик сделал небольшие открытия в области механики и дал понятие удельному весу тел.

Евклид

К IVIII векам до нашей эры геометрия вполне оформилась как наука. Были устоявшиеся традиции, детально разработанные методы решения задач, крупные достижения, было уже несколько учебников и различные научные школы.

Рассказать обо всех геометрах доевклидового периода а список математиков того времени включает несколько десятков славных имён и об их работах, естественно, невозможно. И поскольку у нас не многотомный исторический труд, а небольшая статья, оставим предтеч и перейдём непосредственно к Евклиду.

Жил и работал он во время весьма любопытное.

В 323 году до нашей эры то ли вследствие острой лихорадки, то ли в результате неумеренного пьянства или просто от доброй порции яда отправился на свидание к отцу своему Зевсу царь царей земных, изрядно уже потрёпанный жизнью, хотя сравнительно молодой, тридцатитрёхлетний мужчина Александр Македонский.

Полубога подобающим образом проводили и перешли к текущим делам. А дел хватало: надо было делить империю. Размеры её были невероятны. Всего лишь за десять лет оказались завоёванными страны, в сотни раз превосходившие маленькую полунищую Македонию.

Границы известного мира расширились во много раз, и теперь предстояло переварить проглоченное. Было ясно, что для одного такое наследство непомерно, и отдавать всё малолетнему брату Александра или же второму наследнику сыну, появившемуся на свет через несколько месяцев после смерти отца, было просто смешно. Посему империю полюбовно растащили те полководцы, которых Александр не успел казнить. Они поклялись в вечной дружбе, заключили вечный мир, порядком выпили на радостях, обменялись суровыми мужскими пожатиями на прощанье и, естественно, началась междоусобная резня.

Более других в этой сваре повезло осмотрительному Птолемею, который при делёжке отхватил себе Египет. Наследники его постепенно ассимилировались, а династия оказалась не только самой прочной и долговечной, но и прославилась тем, что дала истории Клеопатру.

И самый первый Птолемей, и все последующие Птолемеи славны тем, что были покровителями наук. Какие у них на то были мотивы, трудно сейчас разобраться, но факты таковы: в IIIII веках до нашей эры Александрия превратилась в основной научный центр эллинистического мира. И наиглавнейшим научным институтом был знаменитый Александрийский музей с Александрийской библиотекой. Сюда-то и пригласил Птолемей Евклида, и именно здесь Евклид написал «Начала» книгу, в истории человечества бесспорно уникальную.

Снова я должен сделать традиционное уже признание: о самом Евклиде практически ничего не известно.

Легенды, конечно же, имеются. Рассказывают, например, что Птолемей поначалу сам захотел одолеть премудрости геометрии, но довольно скоро обнаружил, что изучение математики требует некоторых усилий. Тогда он призвал Евклида и вопросил его, полагаю, как джентльмен джентльмена, нельзя ли постигнуть все тайны науки как-нибудь попроще? На что Евклид ответил: «В геометрии нет царского пути». Остаётся неведомым, продолжал ли после этого царь занятия математикой (вероятнее всего, он утешился в занятиях, более приличествующих царям, таких, как приёмы, охота, пиры, услады гарема, наконец).

Рассказывают также, что однажды к Евклиду явился изучать геометрию некий молодой прагматик. Первый вопрос, который он задал будущему учителю, был следующий: какая практическая польза будет от штудирования «Начал»? Тогда Евклид, весьма и весьма задетый, призвал раба и сказал: «Дай ему обол (грош), он ищет выгоды, а не знаний».

Надо, впрочем, сознаться, что обе истории столь традиционны, учитывая представление древних греков о мудрецах и о математике, что особо доверять им не приходится. «Точные» же биографические данные основываются на заметках неизвестного арабского математика XII века: «Евклид, сын Наукрата, сына Зенарха, известный под именем Геометра, учёный старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира…»

Всё.

Человек бесследно растворился в веках. Осталась его работа.

Важность

Перед тем была представлена Бельтрами, Клейном и Пуанкаром в модели неевклидовой плоскости, геометрия Евклида стояла неоспоримую как математическая модель в пространстве . Более того, поскольку суть предмета в синтетической геометрии была главным проявлением рациональности, евклидова точка зрения представляла абсолютный авторитет.

Открытие неевклидовой геометрии имело волновой эффект, выходящий далеко за рамки математики и естественных наук. Отношение философа Иммануила Канта к человеческому знанию сыграло особую роль в геометрии. Это был его главный пример синтетического априорного знания; не выведенные из органов чувств и не выведенные с помощью логики — наши знания о космосе были истиной, с которой мы родились. К несчастью для Канта, его концепция этой неизменно истинной геометрии была евклидовой. На богословие также повлиял переход от абсолютной истины к относительной истине в том, как математика соотносится с окружающим миром, что явилось результатом этой смены парадигмы.

Неевклидова геометрия является примером научной революции в истории науки , когда математики и ученые изменили свой взгляд на свои предметы. Некоторые геометры называли Лобачевского « Коперником геометрии» из-за революционного характера его работ.

Существование неевклидовой геометрии во многом повлияло на интеллектуальную жизнь виклидской Англии и, в частности, было одним из ведущих факторов, вызвавших пересмотр преподавания геометрии, основанного на Элементах Евклида . В то время этот вопрос об учебной программе горячо обсуждался и даже стал предметом книги « Евклид и его современные соперники» , написанной Чарльзом Латвиджем Доджсоном (1832–1898), более известным как Льюис Кэрролл , автором « Алисы в стране чудес» .

Фалес

Предполагают, что геометрию начинала Ионийская школа, а точнее, сам её основатель Фалес Милетский, проживший что-то около сотни лет (640540 или 546 годы до нашей эры).

Толком мы мало что знаем о нём.

Точно известно, что имел он титул одного из семи мудрецов Греции, что по официальному счёту идёт как первый философ, первый математик, первый астроном и вообще первый по всем наукам в Греции. По-видимому, он был тем же для Греции, что Ломоносов для России. В молодости Фалес попал в Египет, куда фараон Псамметих только-только начал допускать иностранцев. Вероятно, он оказался там по торговым делам известно, что свою карьеру Фалес начинал купцом.

В Египте Фалес застрял на много лет, изучая науки в Фивах и Мемфисе. Потом он вернулся домой и основал философскую школу, выступая, очевидно, не столько как самостоятельный мыслитель, сколько как популяризатор египетской мудрости.

Считается, что геометрию и астрономию привёз именно он.

Что именно сделал он в геометрии, мы можем только гадать, хотя греческие авторы приписывали ему довольно много.

Например, Прокл Диддох утверждает, что Фалес доказал теоремы о равенстве вертикальных углов, о равенстве углов при основании равнобедренного треугольника, о том, что диаметр делит круг пополам и ещё ряд других.

Допустив даже, что все историки писали сущую истину, мы не можем сказать, самостоятельно ли Фалес пришёл к этим теоремам или просто пересказал идеи египтян.

По-видимому, единственный бесспорный факт из его научной деятельности предсказание солнечного затмения 585 года до нашей эры. Но легенд о Фалесе ходило множество, и это само по себе доказывает, что учёный он был крупный.

Во всяком случае, одному у него могут поучиться все философы: краткости. Полное собрание его сочинений (разумеется, до нас не дошедшее) по преданию составляло всего 200 стихов.

Краткая биография

Биография Евклида до конца не изучена, к примеру, до сих пор неизвестен год рождения. Известно, что он появился на свет в небольшом районе Афин и был платоновским учеником.

Подъем его научной работы пришелся на правление Птолемея Первого. Некоторые сведения о его жизни можно проследить по арабским рукописям и архимедовым письмам к друзьям. Так, по ним можно определить, что Евклид был сыном греческого ученого и жил около Тира в Сирии.

С малых лет получал знания о мире от своего отца, он же привил сыну любовь к естественным наукам, а затем Евклид поступил в школу Платона, где и обучился математическим основам.

Повзрослев, его пригласили в храм Мусейон (по другим данным он был одним из его основателей), в котором собирались видные ученые с поэтами. Тут были классы для занятий. Также храм был заполнен садами с башнями астрономии, помещениями для одиноких размышлений и большой библиотекой.

В Мусейоне он смог открыть школу с лучшими математиками и монументальный труд в области математики, в котором заложил планиметрические основы со стереометрией, теорией чисел, законами алгебры, методами нахождения площадей с объемами и др.

Фрагмент папируса с текстом «Начал» Евклида

Монументальный труд — публикация «Начала». Это серия из 13 книг, представляющая собой обработанные публикации древнегреческих математиков с пятого по четвертый век до нашей эры.

Кроме «Начал», было создано еще одно сочинение — «Данные», в котором были опубликованы основы по геометрическому анализу. Кроме того, александрийский ученый создал учебник, с помощью которого в то время и сейчас изучают астрономию, перспективу, отражение в зеркале, музыкальные интервалы и решают тригонометрические задачи.

Все оставшиеся годы жизни посвятил изучению естественных наук и математических законов, отчего его называют отцом геометрии. О других аспектах его жизни неизвестно до сих пор. Умер в Александрии.

Это интересно: 231,ДУХОВНАЯ КУЛЬТУРА — разбираемся внимательно

История развития геометрии

Самые первые понятия в геометрии люди приобрели еще в глубокой древности. Возникала необходимость определять площади участков земли, объемы различных сосудов и помещений и другие практические потребности. Свое начало история развития геометрии, как науки, берет в Древнем Египте около 4 тысяч лет назад. Затем знания египтян позаимствовали древние греки, которые применяли их преимущественно для того, чтобы измерять площади земельных участков.  Именно с Древней Греции берет свое начало история возникновения геометрии, как науки. Древнегреческое слово «геометрия» переводится, как «землемерие».

Греческие ученые  на основе открытия множества геометрических свойств смогли создать стройную систему знаний по геометрии. В основу геометрической науки были положены простейшие геометрические свойства, взятые из опыта. Остальные положения науки выводились из простейших геометрических свойств с помощью рассуждений. Вся эта система была опубликована в завершенном виде в «Началах» Евклида около 300 года до нашей эры, где он изложил не только теоретическую геометрию, но и основы теоретической арифметики. С этого источника также начинается и история развития математики.

Однако в труде Евклида ничего не сказано ни об измерении объема, ни о поверхности шара, ни об отношении длины круга к его диаметру (хотя присутствует теорема о площади круга). История развития геометрии получила продолжение в середине III века до нашей эры благодаря великому Архимеду, который смог вычислит число Пи, а также смог определить способы вычисления поверхности шара. Архимед для решения упомянутых задач применил методы, которые в дальнейшем легли в основу методов высшей математики. С их помощью он уже мог решать трудные практические задачи геометрии и механики, которые были важны для мореплавания и для строительного дела. В частности, он нашел способы определять центры тяжести и объемы многих физических тел и смог изучить вопросы равновесия тел различной формы при погружении в жидкость.

Древнегреческие ученые провели исследования свойств различных геометрических линий, важных для теории науки и практических применений. Аполлоний во II веке до нашей эры сделал много важных открытии по теории конических сечений, которые оставались непревзойденными на протяжении следующих восемнадцати веков. Апполоний применил метод координат для изучения конических сечений. Этот метод в дальнейшем смогли развить только в XVII веке ученые Ферма и Декарт. Но они применяли этот метод только для изучения плоских линий. И только в 1748 году русский академик Эйлер смог применить этот метод для изучения кривых поверхностей.

Система, разработанная Евклидом, считалась непреложной более двух тысяч лет. Однако в дальнейшем история развития геометрии получила неожиданный поворот, когда в 1826 году гениальный русский математик Н.И. Лобачевский смог создать совершенно новую геометрическую систему. Фактически основные положения его системы отличаются от положений геометрии Евклида только в одном пункте, но именно из этого пункта вытекают основные особенности системы Лобачевского. Это положение о том, что сумма углов треугольника в геометрии Лобачевского всегда меньше 180 градусов. На первый взгляд может показаться, что это утверждение неверно, однако при маленьких размерах треугольников современные средства измерения не дают правильно измерить сумму его углов.

Дальнейшая история развития геометрии доказала правильность гениальных идей Лобачевского и показала, что система Евклида просто неспособна решить многие вопросы астрономии и физики, где математики имеют дело с фигурами практически бесконечных размеров. Именно с трудами Лобачевского уже связано дальнейшее развитие геометрии, а с ней и высшей математики и астрономии.

«Начала» Евклида

Главный труд Евклида – «Начала» (или «Элементы», в оригинале «Стойхейа»). «Начала» Евклида состоят из 13 книг. Позднее к ним были прибавлены еще две книги.

Первые шесть книг «Начал» посвящены геометрии на плоскости – планиметрии. В философско-теоретическом отношении, в плане философии математики особенно интересна первая книга, которая начинается с определений, постулатов и аксиом, учение о которых было заложено Аристотелем.

Евклид определяет точку как то, что не имеет частей. Линия – длина без ширины. Концы линии – точки. Прямая линия равно расположена по отношению к точкам на ней. Поверхность есть то, что имеет только длину и ширину. Концы поверхности – линии. Плоская поверхность есть та, которая равно расположена по отношению к прямым на ней. И так далее. Таковы определения Евклида.

Статуя Евклида в музее Оксфордского университета

Далее следуют постулаты, т. е. то, что допускается. Допустим, что от всякой точки до всякой точки можно провести прямую линию, что ограниченную прямую можно непрерывно продолжить по прямой, что из любой точки, принятой за центр, можно всяким раствором циркуля описать круг, что все прямые углы равны между собой и что если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то, будучи продолженными, эти две прямые рано или поздно встретятся с той стороны, где углы меньше двух прямых.

Аксиомы Евклида говорят о том, что величины, равные третьей величине, равны между собой, что если к равным прибавить равные, то и целые будут равными, и т. д.

Далее, в первой же книге «Начал» Евклида, рассматриваются треугольники, параллельные линии, параллелограммы. Вторая книга «Начал» содержит геометрическую алгебру: числа и отношения чисел выражаются в пространственных величинах и в их пространственных же отношениях. Третья книга «Начал» исследует геометрию круга и окружности, четвертая – многоугольники. Пятая книга дает теорию пропорций как для соизмеримых, так и для несоизмеримых величин. В книге VI Евклид прилагает эти теории к планиметрии. Книги VII – X содержат теорию чисел, причем X книга трактует иррациональные линии. XI, XII и XIII книги «Начал» посвящены стереометрии, при этом в XII книге применяется метод исчерпания.

В строгом смысле слова Евклида нельзя считать «отцом геометрии». Свои «Начала» были у Гиппократа Хиосского в V в. до н. э. В IV в. до н. э. «Начала» были у Леона, и у Феудия Магнесийского. Метод исчерпания применял Евдокс Книдский, возможный учитель Евклида по Академии. Проблемой иррациональности занимались пифагореец Гиппас Метапонтский, Феодор Киренский, Теэтет Афинский… Однако Евклид – не простой передатчик сделанного до него математиками. В «Началах» Евклида мы видим завершение математики как стройной науки, исходящей из определений, постулатов и аксиом и построенной дедуктивно. Математика Евклида – вершина древнегреческой дедуктивной науки. Она резко отличается от ближневосточной математики с ее практической приблизительной рецептурностью. Не случайно «Начала» Евклида по их логической стройности, ясности, изяществу и законченности сравнивают с .

Правда, существовала легенда, что сам Евклид – не единственный автор дошедших до нас «Начал», что он сам дал лишь догматическое изложение материала, без доказательств, что доказательства были добавлены вышеупомянутым Теоном Александрийским. Теон Александрийский действительно занимался проблематикой «Начал». Но не он один. Этим же занимались и Прокл, и Симплиций. «Начала» Евклида были частично переведены на латинский язык Цензорином и Боэцием. Но эти их переводы затерялись. На Западе вплоть до конца XII в. находились в обращении тезисы Евклида без доказательств.

Что касается Ближнего Востока, то там Евклид был известен в переводах с греческого на сирийский, а с сирийского – на арабский. Первым арабским философом, который заинтересовался Евклидом, был, по-видимому, аль-Кинди (IX в.). Его интерес ограничивался евклидовой «Оптикой». Однако затем последовала масса переводов и комментариев на «Начала». Эти арабские тексты были переведены в XIII в. на латинский язык. Первый латинский перевод с греческого оригинала был делан в Европе в 1493 г. и отпечатан в 1505 г. в Венеции. Но до 1572 г., когда Федерико Коммандино в своем латинском переводе исправил эту ошибку, Евклида-математика путали с Евклидом Мегариком.

Архитектура и геометрия

Геометрические принципы внедрены во все проекты архитектурных сооружений. Неоспорима решающая роль геометрии при строительстве любых зданий.

Строительное проектирование всегда производится с учетом пространственных форм, влияющих на зрительное восприятие и относящихся к важнейшим характеристикам любого здания.

Геометрический вид, являющийся важным свойством сооружения и определяемый трехмерными размерами (ширина, глубина, высота), зависим от их соотношения. При равных размерах – форма архитектурного сооружения выглядит объемной, при одном из размеров значительно меньшем, чем два остальных – сооружение выглядит плоским, а в случае, когда два размера намного менее одного, сооружение приобретает линейный вид.

Архитектурные свойства определяются протяженностью по трем координатным осям и характеризуются размерами по высоте, ширине и глубине относительно размеров человека или смежных строений.

Рекомендации

• А’Кампо, Норберт и Пападопулос, Атанас , (2012) Заметки о гиперболической геометрии , в: Страсбургский мастер-класс по геометрии, стр. 1–182, Лекции IRMA по математике и теоретической физике, Vol. 18, Цюрих: Европейское математическое общество (EMS), 461 страница, ISBN  978-3-03719-105-7 , DOI: 10.4171 / 105 .
• Андерсон, Джеймс В. Гиперболическая геометрия , второе издание, Springer, 2005 г.
• Бельтрами, Eugenio Teoria fondamentale degli spazî di curvatura costante , Аннали. ди Мат., серия II 2 (1868), 232–255
• Блюменталь, Леонард М. (1980), Современный взгляд на геометрию , Нью-Йорк: Довер, ISBN 0-486-63962-2
• Кэрролл, Льюис Евклид и его современные соперники , Нью-Йорк: Барнс и Ноубл, 2009 (перепечатка) ISBN  978-1-4351-2348-9
• HSM Coxeter (1942) Неевклидова геометрия , University of Toronto Press , переиздано в 1998 году Математической ассоциацией Америки , ISBN  0-88385-522-4 .
• Фабер, Ричард Л. (1983), Основы евклидовой и неевклидовой геометрии , Нью-Йорк: Марсель Деккер, ISBN 0-8247-1748-1
• Джереми Грей (1989) Идеи пространства: евклидово, неевклидово и релятивистское , 2-е издание, Clarendon Press .
• Гринберг, Марвин Джей Евклидова и неевклидова геометрия: развитие и история , 4-е изд., Нью-Йорк: WH Freeman, 2007. ISBN  0-7167-9948-0
• Моррис Клайн (1972) Математическая мысль от древних до наших дней, глава 36, Неевклидова геометрия, стр. 861–81, Oxford University Press .
• Бернард Х. Лавенда , (2012) «Новый взгляд на теорию относительности: одиссея в неевклидовой геометрии», World Scientific , стр. 696, ISBN   .
• Николай Лобачевский (2010) Пангеометрия , переводчик и редактор: А. Пападопулос, Серия «Наследие европейской математики», Vol. 4, Европейское математическое общество .
• Мэннинг, Генри Паркер (1963), Введение в неевклидову геометрию , Нью-Йорк: Дувр
• Мешковский, Герберт (1964), Неевклидова геометрия , Нью-Йорк: Academic Press
• Милнор, Джон В. (1982) , Bull. Амер. Математика. Soc. (NS) Том 6, номер 1, стр. 9–24.
• Ричардс, Джоан Л. (1988), Математические видения: стремление к геометрии в викторианской Англии , Бостон: Academic Press, ISBN 0-12-587445-6
• Смарт, Джеймс Р. (1997), Современная геометрия (5-е изд.) , Pacific Grove: Brooks / Cole, ISBN 0-534-35188-3
• Стюарт, Ян (2001) Флаттерленд , Нью-Йорк: ISBN  издательства Perseus 0-7382-0675-X ( мягкая обложка )
• Джон Стиллвелл (1996) Источники гиперболической геометрии , ISBN Американского математического общества 0-8218-0529-0 . 
• Трюдо, Ричард Дж. (1987), , Бостон: Birkhauser, ISBN 0-8176-3311-1
• A. Papadopoulos et Guillaume Théret (2014) La théorie des parallèles de Johann Heinrich Lambert , (Критическое издание мемуаров Ламбера с французским переводом, с историческими и математическими примечаниями и комментариями — изд. Blanchard, Coll. Sciences dans l’Histoire, Paris ISBN  978-2-85367-266-5

Свойства треугольников

Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.

Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника. Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет

Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок

Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.

Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.

Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.

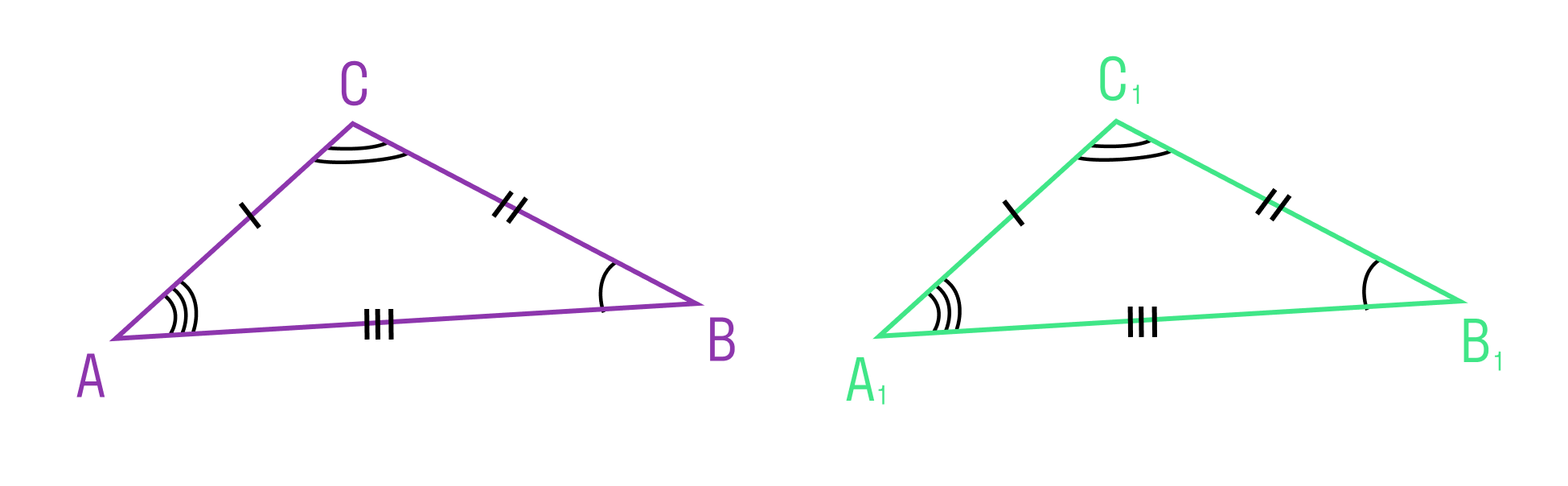
Равенство треугольников ABC и A₁B₁C₁ обозначается так: ΔABC = ΔA₁B₁C₁.

Есть даже специальные теоремы про равенство треугольников.

Первый признак равенства треугольников звучит так:

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны

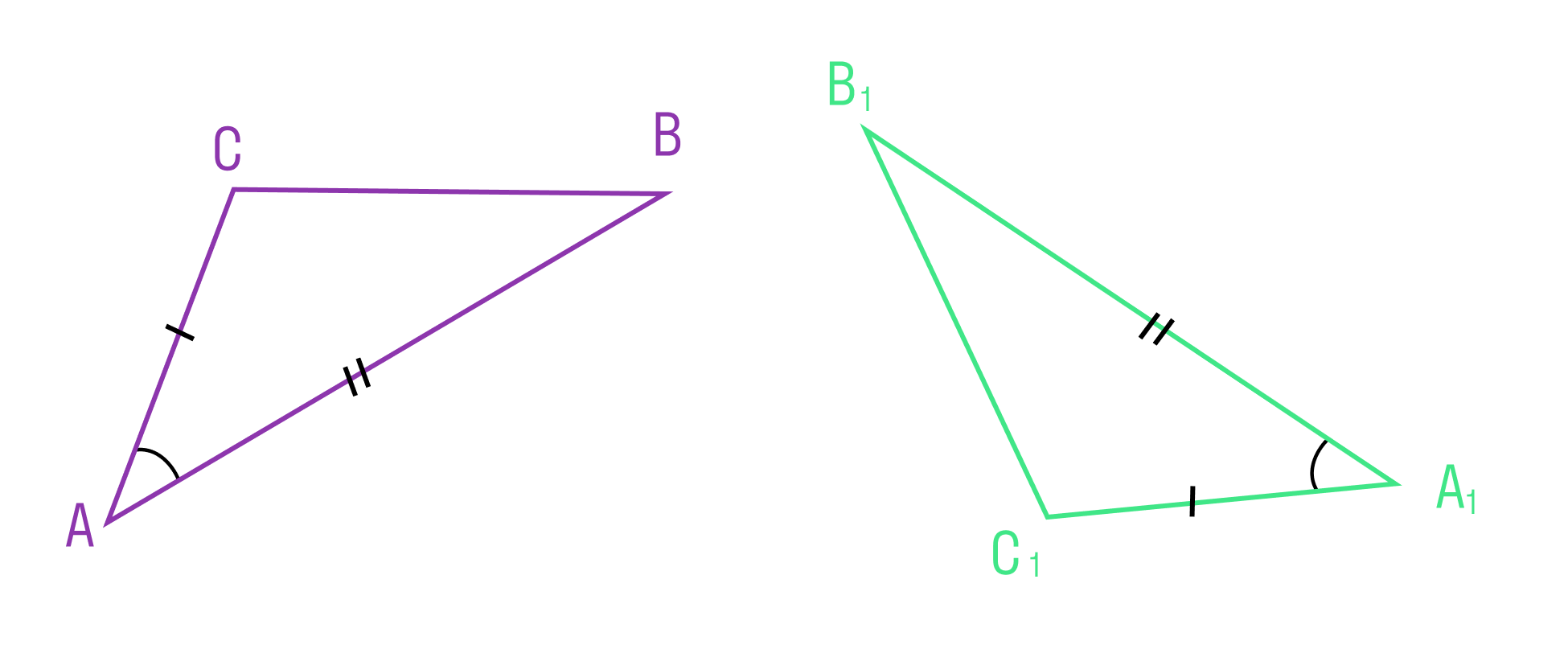
ΔABC = ΔA₁B₁C₁, так как AC = A₁C₁, AB = A₁B₁ и ∠A = ∠A₁ (∠A лежит между сторонами AC и AB, а ∠A₁ между A₁C₁ и A₁B₁).

Второй признак равенства треугольников

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

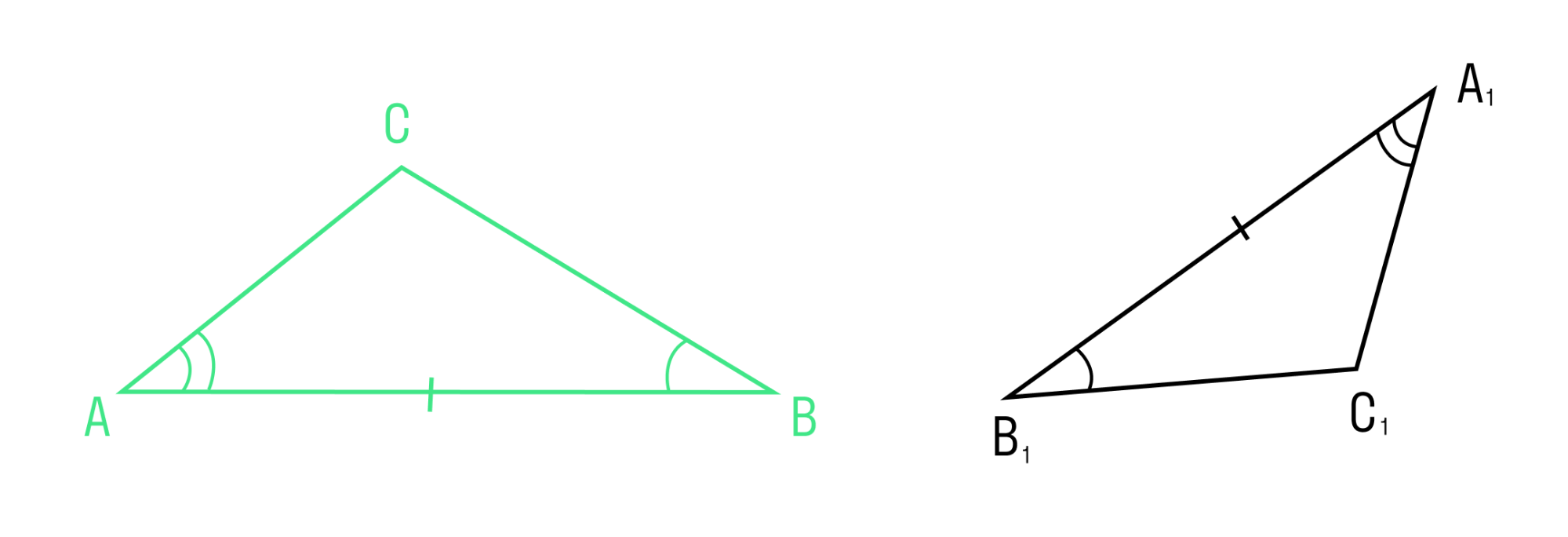
ΔABC = ΔA₁B₁C₁, так как AB = A₁B₁,  ∠A = ∠A₁, ∠B = ∠B₁.

Третий признак равенства треугольников

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

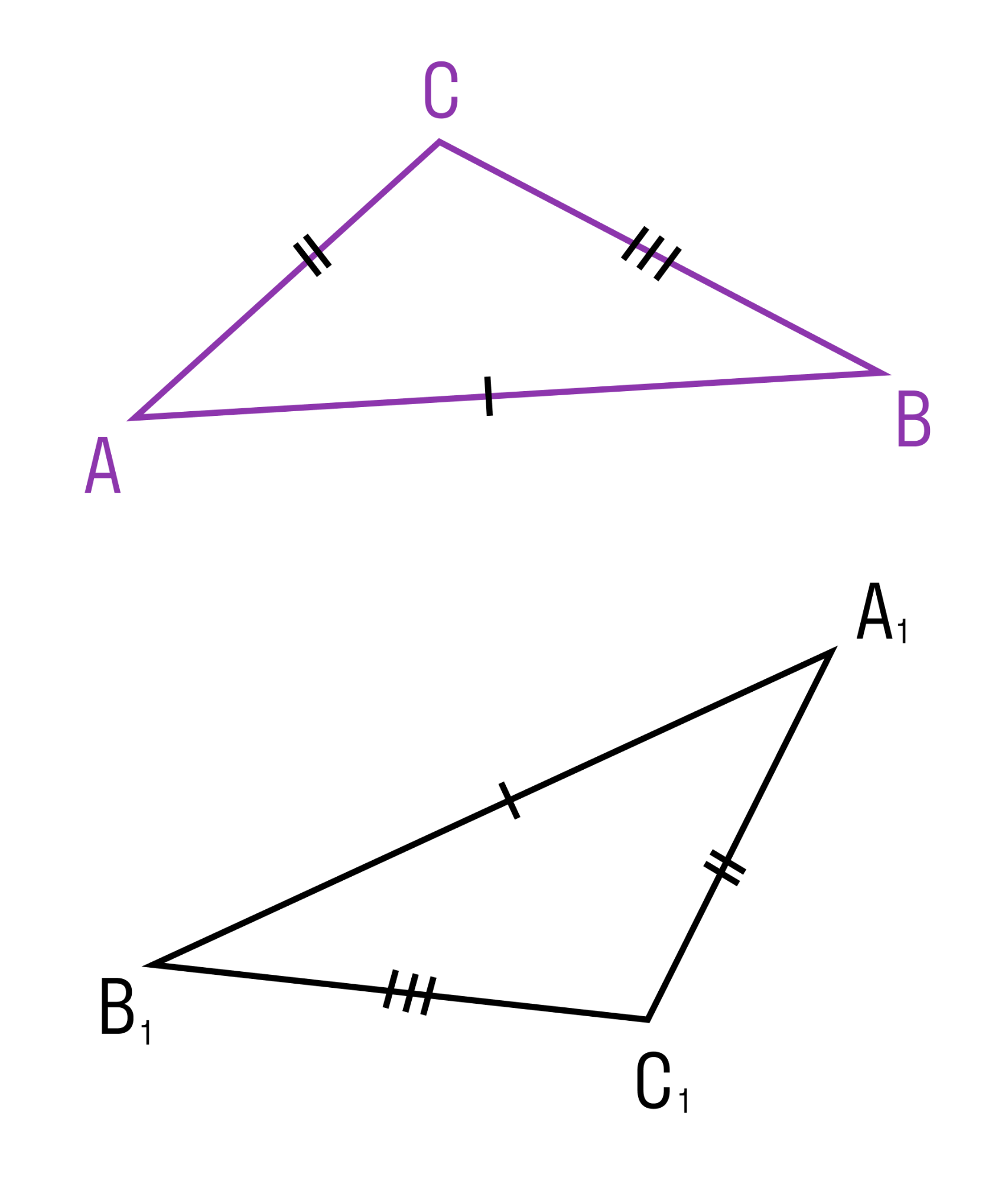
ΔABC = ΔA₁B₁C₁, так как AC = A₁C₁, AB = A₁B₁ и BC = B₁C₁.

Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.

Достижения Евклида

Достижения Евклида имели огромное значение для мировой истории, математики и других наук.

Он был первым, кто:

• систематизировал известные труды предшественников в единый сборник из 13 книг;
• создал 5 постулатов НОД и 5 аксиом в области геометрии;
• охарактеризовал все известные геометрические фигуры, дал понятие кривым линиям, коническим сечениям и другим явлениям;
• создал трактат по ошибкам при изучении и создании геометрических доказательств;
• доказал практическое использовании математики при изучении звезд, небесных тел, космоса и других наук;
• изучил свет с законами его распространения;
• изучил зеркала и способности преломления в них световых лучей;
• создал простейшую теорию в области музыки;
• создал постулаты и формулы по механики и определил удельный вес тел.

Математика

Евклид — отец математики. Он сформулировал теоремы по планиметрии, упростил понимание теоремы Пифагора и теоремы о сумме углов треугольника, прописал свойства правильных многоугольников и законы построения правильных пятнадцатиугольников, указал, как применима алгебры в жизни и каковы ее основные теории, вписал теорию о целом и рациональном числе, рассмотрел квадратичную иррациональность, заложил основы стереометрической науки, доказал теоремы, касающиеся площади круга с объемом шара, вывел отношение объема пирамид с конусами, призмами и цилиндрами.

Другие науки

Помимо математики, ученый работал с оптикой, астрономией, логикой и музыкой. Так, в оптике он дал сведения об оптической перспективе, зеркальных искажениях и отражениях световых лучей в зеркале.

Первые следы геометрии

Мегалитный треугольник Валле-ди-Леванте в Фондачелли Фантина , Сицилия

Хотя можно считать основоположниками геометрии как науки и математической дисциплины, обширные знания в области геометрии, необходимые для топографии , архитектуры , астрономии и сельского хозяйства , возникли еще до греческой цивилизации. Первые признанные понятия геометрии относятся к 3000 году до нашей эры. Н.э. , со времен Древнего Египта , древней индуистской цивилизации, вавилонян и, возможно, (но гипотеза остается спорной) мегалитических народов Великобритании и Британии.

Египетская и вавилонская геометрии

Отрывок из папируса Ринда — около 1650 г. до н.э. Британская Колумбия — Британский музей

Египетские пирамиды и планы орошения свидетельствуют, по крайней мере, об эмпирическом знании плоских и твердых фигур. Немногочисленные оставшиеся документы ( папирус Москва , папирус Райнда , папирус Кахун ) показывают использование практических правил для решения конкретных вопросов, связанных с понятиями длины угла , площади и объема .

Похоже, что геометрия появилась у египтян в результате необходимости, с которой они сталкивались каждый год, исследовать земли, преобразованные в результате наводнений Нила. Затем он развивался для нужд архитектуры , сельского хозяйства и астрономии .

Предварительно вавилонская таблетки ЕКЗ 7289 начиная с -1700 ± 100 свидетельствует первые вопросы о расчете длины и дает хорошее приближение длины диагонали квадрата (квадратный корень из 2).

Среди результатов этих древних наук мы можем привести варианты теоремы Пифагора , разработанные египтянами и вавилонянами за 1500 лет до пифагорейцев, таблицу тригонометрии у вавилонян или точную формулу для объема усеченной квадратной пирамиды.

Индийская геометрия (3000-500 гг. До н.э. )

Цивилизации долины Инда использовали геометрические выводы, разработанные как их современники в Месопотамии и Египте.

Геометрия практикуется в Индии с тех пор, и индийский математик VII — го  века Брахмагупты , которому приписывают изобретение нуля , также автор теоремы, носящей его имя . Более того, вклад Индии в развитие тригонометрии также весьма значителен (см. История тригонометрических функций ).

Китайская геометрия

Девять глав математического искусства

Девять глав по математическому искусству , фундаментальный текст знаний о китайской цивилизации, предлагают вычисления площадей и объемов, а также формулировку теоремы Пифагора. Они были подготовлены к I — го или II — го  века  до нашей эры. AD .

Наглядное доказательство теоремы Пифагора